Microtonality is one of those seemingly deeply esoteric terms that both mystifies and terrifies musicians. The purpose of this series is to open the door of understanding to the world of microtonality and, ultimately, intonation. The question of how to achieve intonation in choral music has plagued conductors for centuries. We struggle with teaching our singers to hear the alignment of harmonies, and training their technique to maintain the pitches they hear.
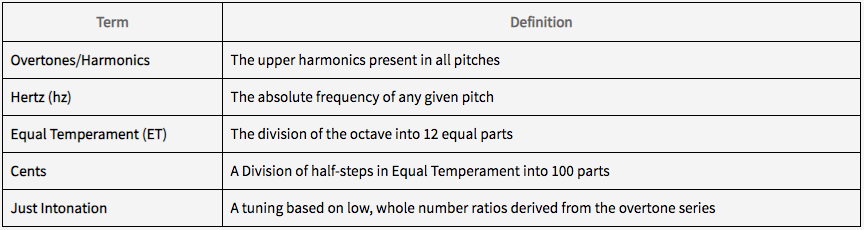
To make sure we’re all on the same page, here’s a list of terms I’ll be using in this series:
Part 2: Just Intonation vs. Equal Temperament, or Why the Piano is Always Out of Tune
For an introduction to intonation and the overtone series, read the previous article in this series here.
All sound vibrates, and within each vibration are a series of smaller vibrations. These smaller, and higher, vibrations are the overtone series, which follows the same pattern. An interesting aspect of the series is that, while the Hz go up by a constant amount, our musical perception is that the intervals get smaller as they get higher. So, if our first pitch is at 100 Hz (we’ll call it a C, though it’s not really) the series will look like this:

Musically it looks like this:

As you can see, the notes of the overtone series don’t fall neatly into a typical scale, or even within a single octave. Instead, each interval between harmonics is an increasingly smaller interval than the one before it, starting with the octave, then 5th, then 4th, and so on. By halving the Hz values of the notes in the overtone series, however, we can get the most consonant octave related pitch. For instance, if 300 Hz is the 3rd overtone (the octave + fifth) 150 Hz will be the perfect fifth. The initial octave is between 100 and 200 hundred Hz, so we’ll need to cut the other notes of the series in half until they fit between these two numbers. For example:

This rational and arithmetic approach to building chords and scales based on the overtone series is referred to as Just Intonation. Because the human ear is geared towards creating consonance, we naturally gravitate towards singing intervals with this kind of intonation. The relationship between these intervals are often expressed in ratios, for instance the major 3rd is a 5/4 ratio (125/100 reduced down) and a perfect fifth would be 3/2.
Equal temperament (ET), on the other hand, organizes the octave to have equal space between each of the notes. ET is how we typically tune fixed pitch instruments like pianos and guitars today. These are also based on ratios, but because of the difference in Hz between different octaves, the ratios aren’t so even looking. Again, let’s use our example of the octave between 100 Hz and 200 Hz. To evenly divide 12 notes between these two pitches we need a ratio of 2x/12 for each half step, with x being the number of half steps away from the original pitch. So 21/12 is the first half step, and 212/12 (again, twice as many Hz) is the octave. The math gets complicated, but trust me when I say this is the Hz breakdown for an ET Chromatic Scale between 100 and 200 Hz:

As you can see, there’s not a lot of rhyme or reason to these numbers. This is because our experience of the musical intervals is logarithmic, not algorithmic. We hear the distance between 100 and 200 Hz as a single octave, but we also hear the distance between 400 Hz and 800 Hz as a single octave, not 4 octaves. To illustrate this point, here is a comparison of pitches derived from the overtone series using the JI method, and Equal Temperament, which is how pianos are tuned:

Clearly we have some discrepancies! What this means for us as listeners is the intervals in Equal Temperament are actually less consonant (or less in tune) than the more perfectly aligned JI method. What it means for us as singers though, is that the piano is a less perfect tuning tool than our own ears. As you can see, most of the intervals are fairly close, but some are quite different. An Equally Tempered minor 7th, for instance, is 31 cents different than in JI, which is very audible. We’ll discuss why this is in the next article in the series, but in short pianos are designed to so that all the intervals are just a little bit out of tune, which allows us to play in any key, rather than having the instrument tuned to a specific one.
Ready to jump deeper into microtonality? Read the NEXT article to learn more about how you can make conscientious tuning choices between different kinds of intervals.

Fahad is the director of See-A-Dot Music Publishing, Inc., a company devoted to the advocacy of new choral works and emerging composers. He is an active performer, composer, and conductor and specializes in contemporary and experimental music, particularly improvisation and the use of extended vocal techniques. He is co-artistic director for the interdisciplinary music/dance company The Resonance Collective, is a founding member of the C3LA: the Contemporary Choral Collective of Los Angeles, and a board member of C4: The Choral Composer/Conductor Collective. He is currently a faculty member, choral director, and doctoral candidate in the performer/composer program at the California Institute of the Arts.


